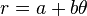Arquímides de Siracusa ( 287 - 212 a.C )

 Arquímedes de Siracusa fue un matemático, físico, inventor, ingeniero y astrónomo griego. Es considerado uno de los mas importantes científicos de la antigüedad clásica.

• Reseña de su vida

Arquímedes nació c. 287 a. C. en el puerto marítimo de Siracusa (Sicilia, Italia), ciudad que en aquel tiempo era una colonia de la Magna Grecia. 


Conociendo la fecha de su muerte, la aproximada fecha de nacimiento está basada en una afirmación del historiador bizantino Juan Tzetzes, que afirmó que Arquímedes vivió hasta la edad de 75 años. 
Según una hipótesis de lectura basada en un pasaje corrupto de El contador de arena, Arquímedes menciona el nombre de su padre, Fidias, un astrónomo sobre el que nada se sabe.
Se sabe que un amigo de Arquímedes, Heráclides, escribió una biografía sobre él pero este libro no se conserva, perdiéndose así los detalles de su vida. Se desconoce, por ejemplo, si alguna vez se casó o tuvo hijos.


Entre los pocos datos ciertos sobre su vida, Diodoro Sículo da uno, según la cual es posible que Arquímedes, durante su juventud, estudiase en Alejandría, en Egipto.
El hecho de que Arquímedes se refiera en sus obras a científicos cuya actividad se desarrollaba en esa ciudad, abona la hipótesis: de hecho, Arquímedes se refiere a Conon de Samos como su amigo en Sobre la esfera y el cilindro, y dos de sus trabajos (El Método de los Teoremas Mecánicos y el Problema del Ganado) están dedicados a Eratóstenes de Cirene.


Arquímedes murió c. 212 a. C. durante la Segunda Guerra Púnica, cuando las fuerzas romanas al mando del general Marco Claudio Marcelo capturaron la ciudad de Siracusa después de un asedio de dos años de duración.

• Algunos Descubrimientos

La Corona de Oro

Una de las anécdotas más conocidas sobre Arquímedes cuenta cómo inventó un método para determinar el volumen de un objeto con una forma irregular. De acuerdo con Vitruvio, Hierón II ordenó la fabricación de una nueva corona con forma de corona triunfal, y le pidió a Arquímedes determinar si la corona estaba hecha sólo de oro o si, por el contrario, un orfebre deshonesto le había agregado plata en su realización. Arquímedes tenía que resolver el problema sin dañar la corona, así que no podía fundirla y convertirla en un cuerpo regular para calcular su masa y volumen, a partir de ahí, su densidad. Mientras tomaba un baño, notó que el nivel de agua subía en la bañera cuando entraba, y así se dio cuenta de que ese efecto podría ser usado para determinar el volumen de la corona. Debido a que el agua no se puede comprimir, la corona, al ser sumergida, desplazaría una cantidad de agua igual a su propio volumen. Al dividir el peso de la corona por el volumen de agua desplazada se podría obtener la densidad de la corona. La densidad de la corona sería menor que la densidad del oro si otros metales menos densos le hubieran sido añadidos.

Sobre la medida de un círculo

En la proposición II, Arquímedes muestra que el valor del número π (Pi) es mayor que 223/71 y menor que 22/7. Esta cifra fue utilizada como aproximación de π a lo largo de la Edad Media e incluso aún hoy se utiliza cuando se requiere de una cifra aproximada.

Sobre las Espirales

El tratado define lo que hoy se conoce como la espiral de Arquímedes. Esta espiral representa el lugar geométrico en el que se ubican los puntos correspondientes a las posiciones de un punto que es desplazado hacia afuera desde un punto fijo con una velocidad constante y a lo largo de una línea que rota con una velocidad angular constante. En coordenadas polares, (r, θ) la elipse puede definirse a través de la ecuación:

Siendo a y b números reales. Este es uno de los primeros ejemplos en los que un matemático griego define una curva mecánica.


Sobre las Esferas y Cilindros


En este tratado,  Arquímedes llega a la conclusión matemática de la que estaría más orgulloso, esto es, la relación entre una esfera y un cilindro cirscunscrito con la misma altura y diámetro. El volumen es  para la esfera, y 2πr³ para el cilindro. El área de la superficie es 4πr² para la esfera, y 6πr² para el cilindro (incluyendo sus dos bases), donde r es el radio de la esfera y del cilindro. La esfera tiene un área y un volumen equivalentes a dos tercios de los del cilindro. A pedido del propio Arquímedes, se colocaron sobre su tumba las esculturas de estos dos cuerpos geométricos.

Pitágoras de Samos (582 - 507 a. C)

Pitágoras de Samos, fue un filósofo y matemático Griego, que ganó un gran reconocimiento por el Teorema de Pitágoras

• Reseña de su vida

Pitágoras nació en la isla de Samos en el año 582 a. C Siendo muy joven de edad viajó a Mesopotamia y Egipto.
Tras regresar a Samos, finalizó sus estudios con Hermodamas de Samos y luego fundó su primera escuela durante la tiranía de Polícrates. Abandonó Samos para escapar de la tiranía de Polícrates y se estableció en Crotona, La Magna Grecia, alrededor del año 525 a. C, en el Sur de Italia, donde fundó su segunda escuela.

Debido al caracter de la Escuela Pitágorica, donde podian intengrarse tanto hombres y mujeres, sin importar razas, religiones o estratos economicos, los Pitágoricos fueron expulsados por los habitantes de Crotona, estableciendose los Pitágoricos en Tarento y formando su Tercera Escuela

• La Escuela Pitágorica

Se les conocia como Pitágoricos a los participantes de la escuela de pensamiento de Pitágoras, ellos afirmaban que la estructura del universo era Aritmetica y Geometrica, este grupo impartia tambien pensamientos politicos (Con tendencia al Partido Dórico), llegaron a acumular mucha fuerza, hasta el Siglo V, donde fueron perseguidos, y muchos murieron.

La Escuela Pitágorica se dividia en dos Sectores, en los Estudiantes, quienes eran los que aprendian las enseñanzas matematicas, religiosas y filosoficas directamente de su Fundador, mientras que los Oyentes eran los que solo podian observar el comportamiento de los pitágoricos.

• Aportes a la Matematica

Dentro de los Pitágoricos, todos los descubrimientos se le atribuian a su Fundador, haciendo indeterminante si fueron creación de un estudiante o de Pitágoras.

Alguno de los descubrimientos que se le atribuyen son:

1. Una prueba del Teorema de Pitágoras: Si bien los pitagóricos no descubrieron este teorema (ya era conocido y aplicado en Babilonia y la India desde hacía un tiempo considerable), sí fueron los primeros en encontrar una demostración formal del teorema. También demostraron el converso del teorema (si los lados de un triángulo satisfacen la ecuación, entonces el triángulo es recto).
2. Ternas Pitágoricas: Es una terna de números enteros (a, b, c) tales que a² + b² = c². Aunque los babilonios ya sabían cómo generar tales ternas en ciertos casos, los pitagóricos extendieron el estudio del tema encontrando resultados como cualquier entero impar es miembro de una terna pitagórica primitiva. Sin embargo, la solución completa del problema no se obtuvo hasta el siglo XIII cuando  Leonardo de Pisa ("Fibonacci") encontró la forma de generar todas las ternas pitagóricas posibles. 
3. Sólidos regulares: Los pitagóricos descubrieron el Dodecaedro y demostraron que sólo existen 5 poliedros regulares.
4. Números Perfectos: Son aquellos números que son iguales a la suma de sus divisores propios (por ejemplo 6=1+2+3). Encontraron una fórmula para obtener ciertos números perfectos pares
5. Números amigables: Un par de números son amigables si cada uno es igual a la suma de los divisores propios del otro. Jamblico atribuye a Pitágoras haber descubierto el par amigable (220, 284).
6. Números Irracionales: El descubrimiento de que la diagonal de un cuadrado de lado 1 no puede expresarse como un cociente de números enteros marca el descubrimiento de los números irracionales.
7. Medias: Estudiaron la relación entre las medias aritmética, geométrica y armónica de dos números y obtuvieron la relación